
Projetos em Destaque
Permutações Montanha-Russa
Estudo de permutações que maximizam a soma \(t(\pi)\) de subsequências crescentes e decrescentes. Minha pesquisa aborda a eficiência computacional e a estrutura dessas permutações.
Contribuições do Artigo (ETC IV - 2021):
- Algoritmo \(O(n^3)\): Redução drástica da complexidade para o cálculo de \(t(\pi)\).
- Modelagem PLI: Uso de Programação Linear Inteira para encontrar roller coasters de maior porte.
- Novos Limites: Superação dos recordes da literatura para \(n \le 40\).
Pico Vale
Imersões de Cliques
Minha pesquisa foca na versão para imersões da célebre Conjectura de Hadwiger, especificamente a variante proposta por Abu-Khzam e Langston.
Destaques do Trabalho (EUROCOMB 2025):
- Estudo de grafos com número de independência \(\alpha(G) = 2\).
- Provamos que se o grau máximo \(\Delta(G)\) é limitado por uma constante \(d\), então \(G\) admite uma imersão de uma clique \(K_t\) onde \(t\) cresce linearmente com o número de vértices \(n\).
- Exploração de como a estrutura de "clusters" em grafos \(\alpha=2\) facilita a construção de caminhos aresta-disjuntos.
📄 Ler Preprint: Immersions of large cliques in graphs... (2025)

Figura 2: Caminhos aresta-disjuntos formando uma imersão de \(K_5\).
Coloração Fortemente Ímpar
Diferente da coloração própria tradicional, a Coloração Fortemente Ímpar exige que para cada vértice \(v\), toda cor que aparece em sua vizinhança, apareça um número ímpar de vezes, além de ser uma coloração própria.
Desafios Teóricos:
- Cálculo do número cromático \( \chi_{so}(G) \) para classes específicas como grafos planares ou grafos com girth elevado.
- Relação entre coloração própria e restrições de paridade em vizinhanças.
- Complexidade computacional para verificar se um grafo admite tal coloração com \(k\) cores.

Figura 3: Coloração fortemente ímpar de um grafo planar com 7 cores.
PydaptiveFiltering Python
PydaptiveFiltering é uma biblioteca em Python para filtros adaptativos (sinais reais e complexos), com API consistente, exemplos reproduzíveis e documentação gerada com pdoc.
- Famílias: LMS, RLS, set-membership, lattice, fast/QR-RLS, IIR, modelos não-lineares e Kalman.
- Baseados no livro "Adaptive Filtering: Algorithms and Practical Implementation" de Paulo S. R. Diniz.
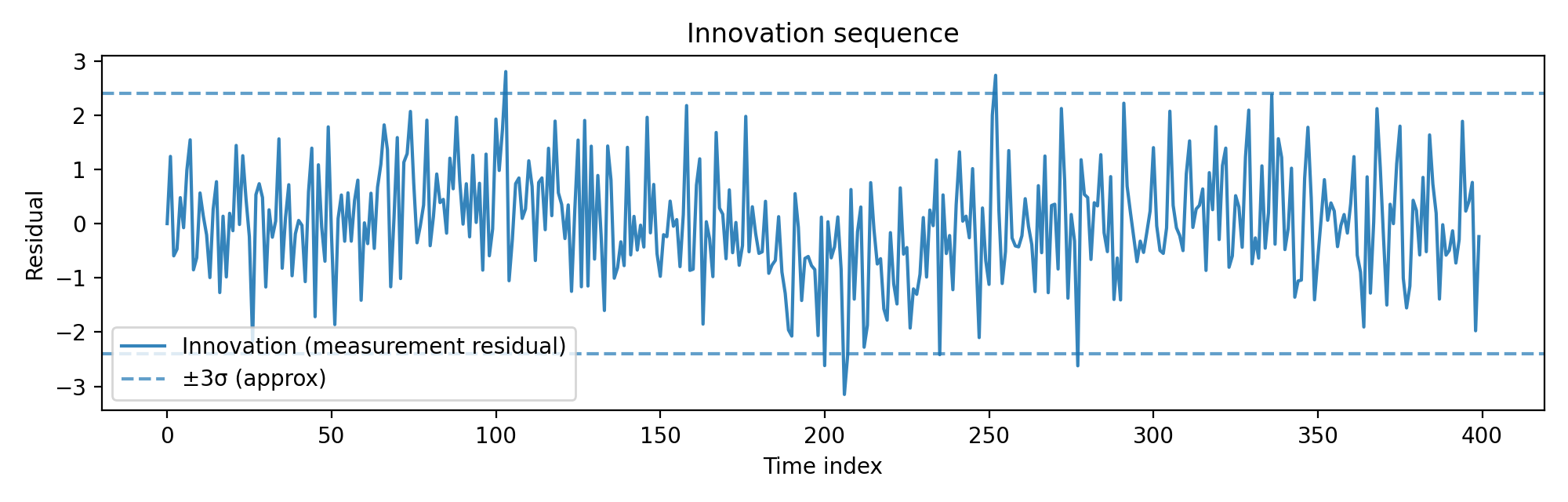
Biblioteca Python para filtros adaptativos (real/complex).
